对我的世界中PVP击退的研究报告

开发经验分享
,

“脚本小子”对MC击退的研究成果

该页面研究的是原版击退算法以及原版击退算法中的各值的作用。

通常我们在调整击退参数的时候，都是靠感觉去调的。Kar团队另辟蹊径，通过数据和代码的方式去理解和调整最合适的击退。为了贯彻我们决心做中国PVP服领头羊的理念，我们决定将我们的研究成果分享出去。

对于代码的分析

EntityLiving类

由于在nms中部分变量经过了混淆，所以只能通过猜测得出这些变量的意义。

在EntityLiving类中，玩家受到伤害时会触发damageEntity函数。

EntityLiving1.png

  • d0为攻击者位置的X值减去受害者位置的X值，即为从受害者到攻击者的向量的X值。
  • d1初始值为攻击者位置的Z值减去受害者位置的X值，即为从受害者到攻击者的向量的Z值。

我们把d0称为x，d1称为z，则

  • 若x²+z²<0.0001，则将d1设为一个-1至1之间的随机值*(见下方)，再乘以0.01，同时将d0也进行一次这样的操作。
  • 若x²+z²还是<0.0001，则再进行一次，直到不满足这个条件为止。

推测，这可能是两个玩家坐标一样或极度相近的时候，为防止产生0变量，生成一个随机的击退。为验证这个猜测，您可以tp一名玩家，此时您的坐标和这名玩家是一模一样的(其实会产生一点点差别)。接着打他一下，发现击退有时候不在您面前的方向，甚至有时候击退到身后去了。

*编个程统计一下这个随机数，进行100000000次(一亿次)模拟，发现其分布曲线是金字塔形。

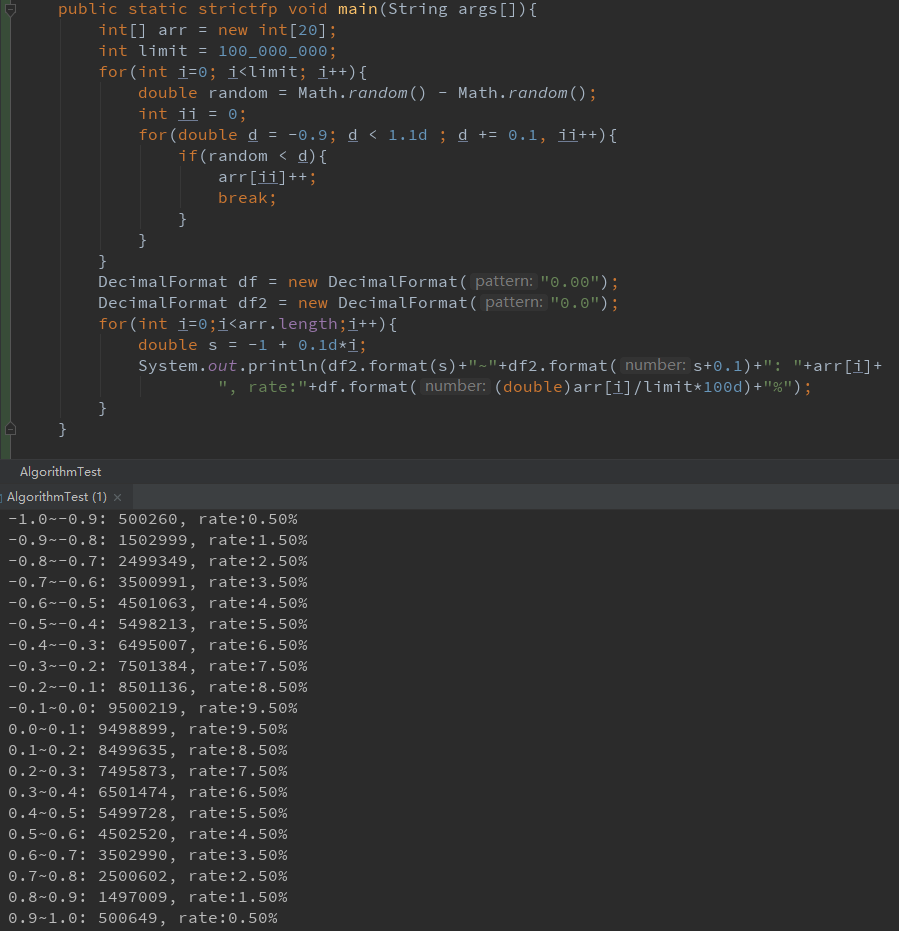
分布是折线.png

它看起来大概是这样：

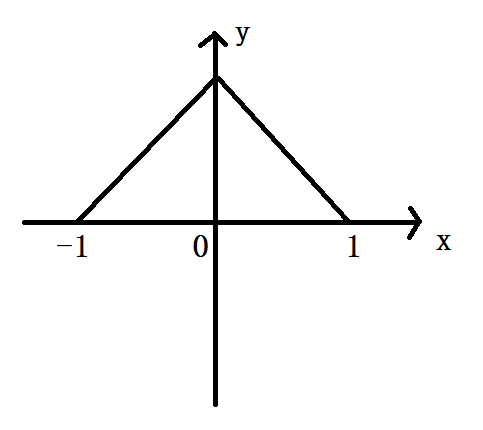
折线.png

设该折线的方程为 y = f(x), x∈(-1, 1)
很明显，该随机变量X落在(-x, x),x∈(0, 1)的几率为

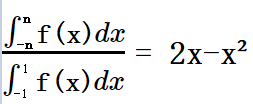
几率.png

几率Latex

1
$\frac{\int_{-n}^{n}f(x)dx}{\int_{-1}^{1}f(x)dx}=2x-x^2$

函数a中

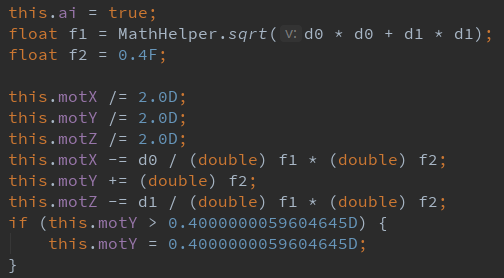
EntityLiving2.png

其中的d0和d1即为上方所提的x和z
设一个变量f1为

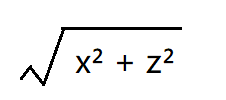
EntityLiving3.png

即为该向量在水平面上投影的距离

  1. 变量f2为0.4，我们把该值称为水平倍数，或者Horizontal
  2. 将motX、motY、motZ分别除以2，我们把该值称为Friction
  3. 接着将motX 减去 x / f1 \* f2
  4. 将motY 加上 f2
  5. 将motZ 减去 z / f1 \* f2
  6. 如果motY大于0.4，则设为0.4(这就是原版击退100附魔也无法飞天只能击远的原因)。我们把该值称为VerticalLimit。

以上即为当受害者受到伤害时的原始击退算法。详细讲解请看下方对原版击退算法的理解。

EntityHuman类

接着在攻击者的算法中，再次对产生的击退做出修正。

在EntityHuman类中,攻击者攻击别人时，受害者会受到以下击退

EntityHuman1.png

其中，i为攻击者手上武器击退附魔的等级，若没有，则为0。
如果攻击者正在疾跑，则i再加1。
但是，在著名服务端mSpigot上，无论攻击者是否在疾跑，i的默认值都为1。

yaw是攻击者的朝向的yaw值(欧拉角警告)，是角度制，所以后面的乘以π除以180是转为弧度制。
entity.g(double motX, double motY, double motZ)函数为

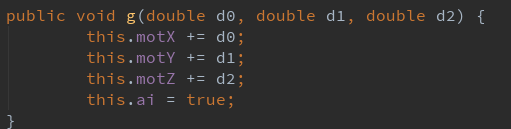
Entity1.png

意思为，该实体目前的速度向量加上这三个值，再把成员ai改为true。
回到上面的击退计算，其中MathHelper是一个优化的数学工具人工具类
于是，该操作可写为

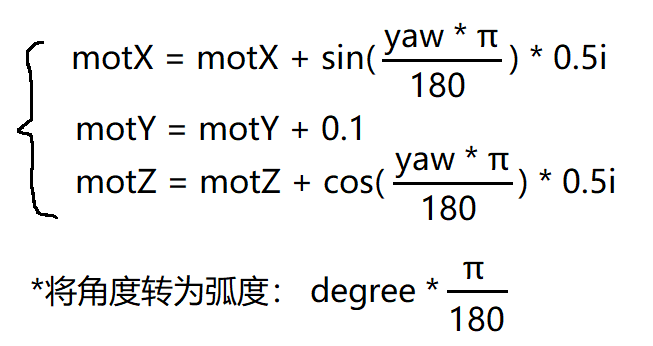
算法1.png

1
2
3
4
5
6
7
$
\begin{cases}
motX=motX+\sin{\frac{yaw*\pi}{180°}*0.5i}\\
motY=motY+0.1\\
motZ=motZ+\sin{\frac{yaw*\pi}{180°}*0.5i}
\end{cases}
$

完成这些操作后，攻击者的motX和motZ各自会乘以0.6。

是攻击者的motX和motZ会乘以0.6！受害者的击退已经算完了，不会乘以0.6缩短！

由于我们平时在竞技场模式中并不会使用带击退附魔的东西当主武器，所以我们不考虑击退附魔。因此，我们只考虑i为0或1的情况。详细讲解请看下方对原版击退算法的理解
我们把上面的0.5i的0.5称为疾跑水平加成(SprintHorizontalBoost[SHB])，motY加的0.1称为疾跑竖直加成(SprintVerticalBoost[SVB])

猜测与实验

玩家的击退对于攻击者的朝向只跟攻击者的yaw值有关，也就是环顾四周时的方向、水平方向有关，和pitch，也就是上下朝向无关。无论攻击者从上往下还是从下往上攻击，击退的原始数值只跟攻击者的yaw值和攻击者与受害者在水平面上的投影的向量有关，接着才根据玩家是否疾跑、武器有无击退、是否对该数值进行进一步计算。
但是，如果攻击者既不在疾跑手上又没有击退附魔，则击退和yaw也无关。

为了证明这一点，在采用原版击退的情况下，我做了个实验。

先将敌人的坐标和自己的坐标精确控制在整数，以便计算。在所有条件都不变的情况下，攻击受害者，计算击退的大小。

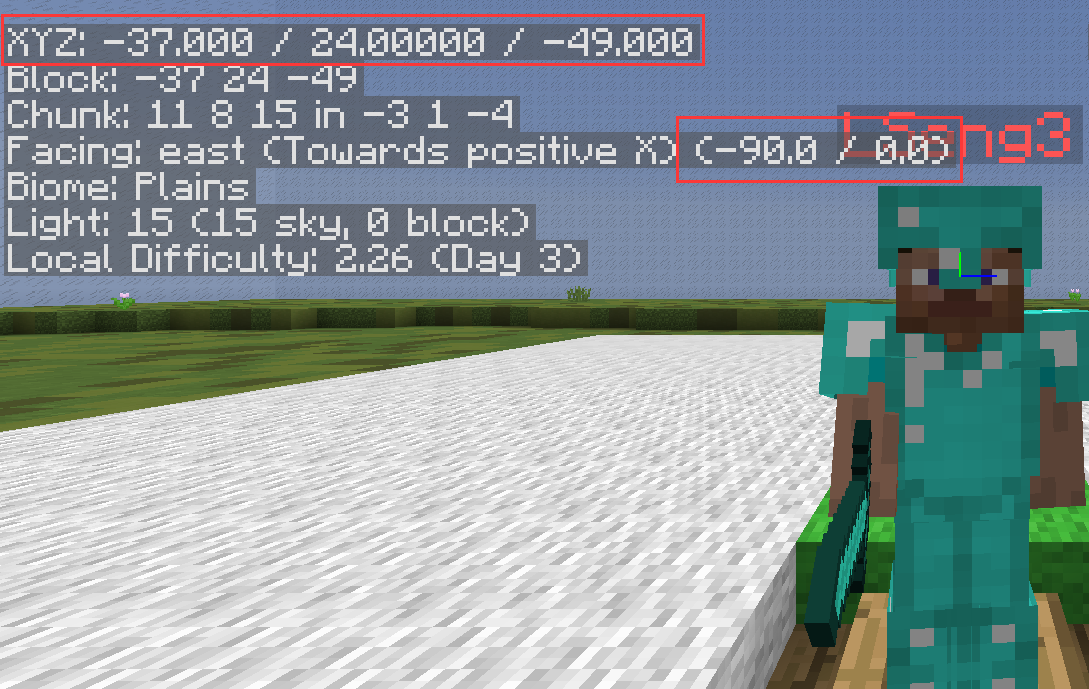
实验1.png

第一次 第二次 第三次
击退前x值坐标 -34 -34 -34
击退后x值坐标 -33.198 -33.198 -33.198

重复3次实验发现，只要条件不变，每次击退都是一样的。

接下来，只改变攻击者的pitch值，其他条件不变。

pitch-> -10 0 10 20 30 40
击退前x值坐标 -35 -35 -35 -35 -35 -35
击退后x值坐标 -33.198 -33.198 -33.198 -33.198 -33.198 -33.198

使用不同的值重复多次实验，发现击退还是一样的。

那么我们只改变攻击者的yaw值，其他条件不变。

yaw-> -100 -95 -90 -85 -80
击退前x值坐标 -35 -35 -35 -35 -35
击退后x值坐标 -33.198 -33.198 -33.198 -33.198 -33.198

神奇的是，yaw值改变后，击退依然不变。

接着，我们给攻击者手上的剑加上击退属性，再进行测试。
同样只改变攻击者的pitch值，发现确实跟攻击者的pitch值无关。

只改变攻击者的yaw值，得出以下结果：

yaw-> -100 -95 -90 -85 -80
击退前x值坐标 -35 -35 -35 -35 -35
击退后x值坐标 -31.034 -31.009 -31.001 -31.009 -31.034
击退前z值坐标 -49 -49 -49 -49 -49
击退后z值坐标 -49.371 -49.182 -49 -48.818 -48.629

多次实验，发现每次结果都与上表相同。在攻击者手上附魔有击退效果时，击退与攻击者的yaw值有关。

我们多测试了如果是受害者yaw、pitch改变是否会影响击退，结果是受害者的朝向完全不影响击退，实验方式和上面差不多，篇幅原因，在此不列出实验详细过程。

测试攻击者疾跑对击退的影响，为了不改变坐标的值，写个插件欺骗服务器，攻击者在攻击时强制变成疾跑状态。测试结果是，疾跑状态攻击相当于手上拿着击退1的武器的效果。

因此我们可以推测，用击退1的武器疾跑着攻击对方，相当于行走状态或静止状态用击退2攻击对方一样。通过实验，证实了该推测。

我们再次推测，在击退与两个玩家的位置和攻击者的yaw值有关，且如果攻击者不在疾跑且手上武器没有击退附魔时，击退就只跟两名玩家的位置有关(除非去掉if(i>0)代码块使motY+0.1强制生效，许多服务端都有这样做)。

用同样的方式，进行以下测试：

  • 测试攻击者与受害者所在位置存在高度差时，击退依然与上面一样，证明击退和高度差无关。
  • 测试攻击者与受害者所在位置的距离不同时，击退依然和上面一样。
  • 测试攻击者向受害者方向走动时攻击，击退依然和上面一样。
  • 测试攻击者跳劈，发现无论是上升状态还是下降状态，击退依然和上面一样。

当受害者在空中时受到攻击，一般击退距离会更远。我们通过编写插件，使玩家站在地上(坐标和上面一样)时欺骗服务器玩家在空中，结果发现击退依然和上面一样。推测因为在空中，在掉落到地面之前有更长的时间在空中滑行，造成的更远击退的感觉。由于方块有Friction属性，也就是当玩家落到地面时速度会迅速降低，而空气的Friction比方块的要低，所以玩家在空中能被击退得更远。

这里所提到的方块Friction跟击退数值中的Friction不一样。

各参数的作用

回到参数上，如果不对原版击退的算法做出改变的话，仅修改算法中的几个参数，我们通常用感觉去判断击退的变化。通过了解上方原版击退的算法后，我们就可以知道那些参数的作用了。

原始击退是指在原始计算中得到的motX、Y、Z的值。目前市面上很多击退插件是在最终击退值上乘以某倍数。

Friction

指在受害者受到攻击时，受到攻击前受害者的速度除以的值，一般大于1，这也是为什么它叫Friction(摩擦)的原因。如果该值等于1，那么此时玩家的速度将会加上击退赋予玩家的速度。如果小于1，则玩家的速度会变大再加上击退赋予玩家的速度。如果大于1，则玩家的速度会先缩短，再加上击退赋予玩家的速度。原版该值为2.0

Horizontal

指原始击退参数的motX、motZ减去值的倍数，原版为0.4

Vertical

指原始击退参数的motY加上的值，原版为0.4

SprintHorizontalBoost, SHB

指最终计算完毕的击退中的motX和motZ在攻击者水平面上所指位置(yaw值所对应位置)加上的，攻击者朝向的向量与x和z轴的投影距离，乘以击退附魔等级+若疾跑加一得到的倍数，再乘以的SHB，即原始数据再加上的击退距离的倍数，原版为0.5

SprintVerticalBoost, SVB

指最终计算完毕的击退中的motY再加上的值，原版为0.1

VerticalLimit

原始击退计算中，最高达到的motY，若超过这个值，则设为这个值。原版为0.4000000059604645

对原版击退算法的理解(硬核慎入)

注意，当玩家静止不动或者站在地面时，他的motY为-0.0784，虽然如此，玩家并没有往下掉，这可能是因为脚下有方块的时候就不往下掉，该值可能是为了制造重力。
这也可以说明，为什么Friction调到很小(如0.01)的时候攻击玩家几乎无击退，因为这时motY除以0.01会变成-7.84，强力压在地上，导致地面对玩家的摩擦力较大，使玩家难以移动。
如果玩家在水中踩到地面，该值为-0.02(也许是重力减去浮力？)

回到一开始，再次看到这个函数

EntityLiving2.png

首先受害者受到了攻击者的一次攻击。在计算击退之前，受害者目前的速度除以Friction以缩短目前的速度(见上方Friction)。通常该值只作用于玩家正在移动的过程中，比如疾跑或者正在被击退。如果玩家是静止的，那么motX和motZ都是0。
如果玩家是在下落状态，则motY是负值，如果这个时候玩家受到攻击，motY会缩小，下落速度会变慢，这也是玩家在空中掉落的过程中受到攻击时会顿一下的原因。

我们知道：

  • d0为攻击者位置的X值减去受害者位置的X值，即为从受害者到攻击者的向量的X值。
  • d1为攻击者位置的Z值减去受害者位置的X值，即为从受害者到攻击者的向量的Z值。
  • f1为从受害者到攻击者的向量在水平面投影的长度。

因此将d0和d1都除以f1后，向量(d0/f1, d1/f1)的模为1。
我们可以把一个长度为1的向量称为单位向量，它通常只为了表示方向。我们将把向量除以它的模的过程称为标准化向量，通常我们在只需要表示向量的方向，长度不重要，且要求该向量模为1的时候这样做。
接着两个值再乘以f2，即乘以0.4，表示把向量乘以0.4，也就是说把向量的模改为 根号0.32 。此时，水平面上的击退原始数据就计算完毕了。

至于为什么motX和motZ是减去运算得出的数值，是因为上面算出来的向量是从受害者指向攻击者的向量，我们需要让受害者往后击退，而不是往攻击者飞过去，所以才是减去。

再看到竖直上的击退，直接是目前的motY加上f2。最后，如果motY超过一个限制值(每错，就是那个小数点后老长的)，就设为那个限制值。您可能会问，才加0.4可能会超过吗？确实会，因为上面说过，在受害者再一次受到伤害前，玩家是飞在空中的。如果是combo模式(即玩家受到攻击后的无敌时间很短)，受害者再一次受到攻击时motY还很大，除以Friction后可能依然很大，所以为防止玩家飞起来就设置了一个限制值。

再来看击退修正，

EntityHuman1.png

entity.g 这个函数可以理解为原速度加上目标速度，如
entity.g(1, 2, 3)就是entity.motX += 1; entity.motY += 2; entity.motZ += 3;
yaw * π / 180就是将玩家朝向的欧拉角yaw值(角度)转为弧度。
在MC中，yaw的范围是-180~179.9。
也就是说，这里的-sin(yaw * π / 180)和cos(yaw * π / 180)依然是生成一个模为1的矢量。为什么模为1？我们把yaw * π / 180设为θ，由sin²θ + cos²θ = 1可知，该向量模为1。
将该向量乘以i 再乘以0.5，即可得到水平上修正的向量。
其中，i默认为0，如果玩家在疾跑状态则+1，如果玩家手上的物品有击退附魔，则再+击退附魔等级。
最后，motY再加0.1。
在原版中，如果i>0，才会执行这段代码，如果i=0，则该代码不被执行，也就是说，motY也不会+0.1。
在著名服务端mSpigot上，由于i默认为1，且疾跑不影响i的值，所以该代码永远会被执行。
最后，把算到的击退交给事件触发器，由事件再次对向量进行更改(如果有的话)，最终将击退速度发送给客户端。

我们可以看到，在算击退原始数据时，击退的方向是以玩家间的位置关系决定的。而在修正的过程中，却由攻击者的yaw值决定。这是印证了上面的实验。所以，如果有个玩家开挂，拿着击退棒背对着打你(请使用不会转过头去打的祖宗级秒被ban外挂实验并关闭反作弊)，你并不会往后退反而往黑客的方向飞去，也是这个道理。

如何抄袭猜测某服务器的击退

如果该服务器的击退数值不是离散的(在相同情况下，击退总是相同，没有产生随机偏移)，且算法为MC原版算法，那么该服的击退数值将非常好猜。

如果击退数值是离散的，那么可以通过统计算出击退数值的分布，然后根据分布的情况模拟随机的数值。比如上方的Math.random() - Math.random()就是-1~1中呈金字塔形的分布，如果是Math.random()-0.5就是在-0.5~0.5比较均匀的分布。除此之外，还有正态分布(new Random().nextGaussian();)等常见分布方式。

我们需要的随机偏移一般不能太大，所以再乘以一个数如0.1缩小随机偏移量的范围。最后根据统计得出的分布规律猜测偏移的算法即可。

由于每次击退服务器只会给你发送一个速度矢量，不可能在击退的过程中持续修正你的速度(不然延迟高的话就会乱飘。速度给你造成的位移一般由客户端计算)。所以，我们只要得出在各种情况下每次服务器发来的击退赋予的速度即可反推击退数值。

为了方便获取击退数值，我特意写了一个mod来辅助您获取某服务器的击退。
版本: 1.8.9
请使用最新版本forge运行以保证兼容性(我们使用的forge版本是forge1.8.9-11.15.1.2318)
当然，别对该mod抱有太大期望，比如按f3会挡住啥的
链接: https://pan.baidu.com/s/11BJ3Rtw-4YTDXECzIXWzAg 提取码: 77f3

这个mod看起来是这样的：

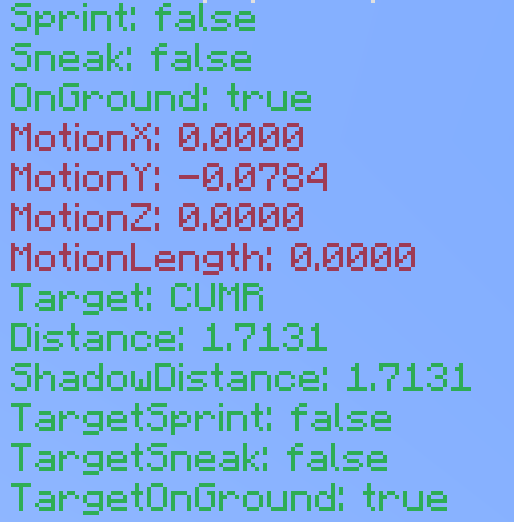
mod.png

什么？你被查端的时候因为这个太像挂端被封了？怪我咯

  • Sprint: 你是否为疾跑状态
  • Sneak: 你是否为潜行状态
  • OnGround: 您是否站在地面
    • 站在地面，指是否落地并站在地面。
    • 如果玩家被击飞、或者跳跃，该值为false。
    • 不过，如果玩家是在飞行状态，即使他的坐标是贴合地面的，OnGround也一定为false。
  • MotionX: 您的速度矢量的X值
  • MotionY: 您的速度矢量的Y值
  • MotionZ: 您的速度矢量的Z值
  • Target: 您正在攻击的玩家的名字
  • Distance: 您与您正在攻击的玩家的距离
  • ShadowDistance: 您与您正在攻击的玩家的连线在水平面上的投影的距离
    • 为什么需要水平面上的投影的距离？如果您有看上方原版击退的算法的话，您就会明白，击退的y值是另算的，玩家之间的位置关系只会决定x和z，y几乎不受玩家间位置影响。
  • TargetSprint: 您正在攻击的玩家是否为疾跑状态
  • TargetSneak: 您正在攻击的玩家是否为潜行状态
  • TargetOnGround: 您正在攻击的玩家是否站在地面

为什么不顺便列出对方的速度矢量？

这是因为对方速度是服务器决定的，服务器只要告诉您对方的位置就可以了。服务端没必要把跟您无关的数据一并发送给您，浪费服务器资源，所以对方的速度矢量无意义。

准备好后，您可以找一个小伙伴，一起装这个mod，然后进入您想测试击退的服务器。接着双方各开启录制~~(建议120帧)~~，模拟出各种情况，然后在视频剪辑软件中看每次攻击时赋予的速度即可。

一定要记住有Friction这个值，也就是每次击退的时候会先削减受害者的速度，再加上计算出来的击退，不然在combo的时候每次值都不一样别以为是random再作祟。

算法区别

你猜测kb的服务器的算法不一定是原版算法，所以当您暴力计算后没得出任何结果的话，您可以再分析总体数据的变化和产生数据对应的情况去猜测算法。即便算法不一定相同，但只要最终算出来的结果是一样的，您的击退和你在抄的服务器的击退就是一样的。

syuu和kar都是使用了不同于原版的击退算法。

然后您可以写一个算法暴力算出误差小于0.0001的击退。

如何防止自己服的kb被盗

使最终计算出来的kb离散化，加上一些微小的随机的偏移，且使用的随机算法也是随机的(不然容易被使用统计方法算出随机算法)。总之，尽量在不影响kb总体感觉的情况下提高猜测kb的难度。

关于本文档

文档的主要研究者与作者: LSeng

文档编写参与者: CarmJos